
Mathematics of Love
17 September, 2023
Finding love can be tough, but math and data can be your allies. Dating apps, driven by machine learning, have gained popularity, with 35% seeking lasting love through them.
The Rational World of Dating Apps
Unlike real-life romance, dating apps rely on deep-learning AI. They analyze user profiles, right swipes, and messaging habits to rank potential matches logically.
The AI Behind It
Collaborative filtering AI models suggest matches similar to past right swipes (item-based) or those favored by similar users (user-based).

Complex Chess Game
Dating apps involve intricate dynamics and algorithms. One notable algorithm is the Gale-Shapley, used not just in dating but also in roommate pairings and matching medical students to residency programs.
Gale-Shapley Algorithm: The Love Matcher
This algorithm, rooted in matching theory, offers a robust solution for finding perfect matches. It's not just for love; it's for pairing people in various scenarios.
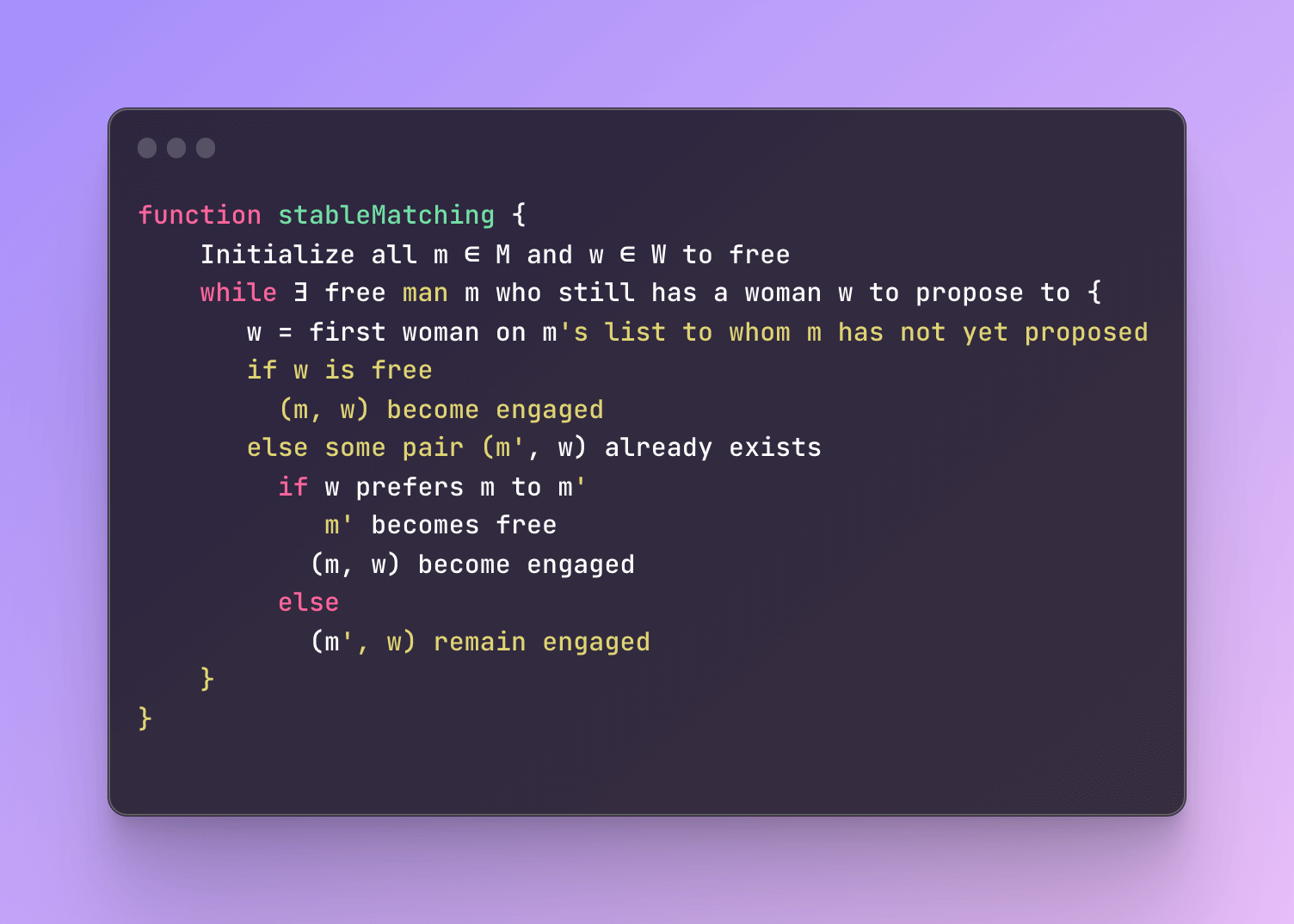
Gale-Shapley Algorithm and Dating Dynamics
The Gale-Shapley algorithm, often used in dating scenarios, favors men as the proposers, following Western tradition. Here's how it works: men propose to their top choices, women tentatively accept their best match, and the process continues until everyone is paired.
Seeking Stability in Matching
A matching is "stable" when no man and woman prefer each other over their current partners. This avoids incentives for pairs to break their matches.
Inherent Bias and Tradition
This algorithm biases the proposing gender, men, which aligns with traditional proposals but can disadvantage women, as they can't choose; they only accept proposals.
The 80-20 Rule in Dating
The Pareto Law, known as the 80-20 rule, applies to dating too. It means that 80% of men compete for 22% of women, while the top 78% of women vie for the top 20% of men. This mirrors a Pareto distribution, indicating high inequality in the "Tinder economy."
Paradox of Choice
Having many options in dating can lead to analysis-paralysis. The "Secretary Problem," a mathematical model, guides us on picking the best option when faced with numerous choices.

The Secretary Problem: Finding Your Ideal Partner with Math
Ever wondered if there's a method to improve your odds of marrying the right person? Turns out, there's a 37% chance this algorithm can help you do just that. While it may not guarantee success, it's definitely better than relying on pure randomness.
The 4-Step Algorithm
Step 1: Estimate the number of potential partners you could date in your lifetime, denoted as 'n.'
Step 2: Calculate the first 37% of people to date, which is 0.37 * n.
Step 3: Date and reject the initial 37% of potential partners; the best among them will set your benchmark.
Step 4: Keep dating people and settle down with the first person who surpasses the benchmark set by the initial 37% of dates.

Optimal Stopping Theory
The logic behind this "optimal stopping theory" is straightforward. Spend time dating, but don't commit until you've gauged the dating landscape. Then, when the time is right, choose the first person who outshines all your previous partners.
Random Choice vs. Strategic Dating
If you opt to settle down randomly without following this strategy, you'd only have a 1/n chance of finding your true love. This translates to just a 5% chance of ending up with your ideal partner if you're expected to date twenty people in your lifetime.
Balancing Patience and Foresight in Dating
When it comes to finding the one to settle down with, there's an important concept to consider: opportunity cost. It's a delicate equilibrium between waiting for the right person and seizing the opportunity before all the great ones are taken.
The Ultimate Dilemma
For those with a mathematical mindset, the question is profound: How do you choose the best person from your current and potential partners without knowing what the future holds? It's a dilemma that requires careful consideration.
Is Finding True Love Possible? The Math Behind It
Many ponder whether finding true love is even possible. Mathematician Peter Backus attempted to answer this question and arrived at a rather dismal conclusion: there might be more intelligent alien civilizations in the galaxy than potential girlfriends for him to date.

Backus' Criteria
Backus considered various factors:
- How many women live nearby? (London had 4 million)
- What's the right age range? (About 20%, or 800,000)
- Are they single? (Around 50%, or 400,000)
- Do they have a university degree? (Approximately 26%, or 104,000)
- Are they attractive? (Roughly 5%, or 5,200)
- Would they find him attractive? (Around 5%, or 260)
- Would they get along well with him? (About 10%, or 26)
Stark Reality vs. Improbable Odds
Based on these criteria and using scientific estimates about life in the universe, Backus found that there are around 400 times more intelligent civilizations on other planets than potential romantic partners.
Fermi Estimation and Beating the Odds
Despite these seemingly improbable circumstances, Backus defied the odds and got married a year after his calculations. This highlights a vital truth: people often end up with partners who don't meet their initial criteria, showing that love can be wonderfully unpredictable.

Happily Ever After: Love and Math in Reality
The quest for "happily ever after" doesn't end when you find your soulmate. A joyful and healthy relationship requires ongoing effort, and how couples handle conflicts can significantly impact long-term happiness.
Mathematical Insights into Love
Mathematics sheds light on the dynamics of love. In happy relationships, negative behaviors are seen as unusual exceptions. Couples maintain a positive view of their partner, reinforcing it with each positive action. In contrast, in strained relationships, bad behavior becomes the norm, while positive actions are viewed as rare occurrences.
John Gottman's Research
Psychologist John Gottman developed a way to quantify positivity and negativity in couples using facial expressions, heart rates, skin conductivity, and blood pressure. His Specific Affect Coding System revealed that successful couples scored far more positive points than negative ones, while struggling couples trended toward negativity. This system accurately predicted divorce rates, with up to 90% accuracy after observing couples in conversation.
Machine Learning for Relationship Prediction
Machine learning models, using couples' responses to specific questions as features, can provide even more accurate predictions about relationships. These applications demonstrate how mathematics can unveil patterns in human behavior, offering valuable insights into the journey of love.
The Relationship Equation: Predicting Love's Course

Gottman and mathematician James Murray uncovered a predictive pattern for relationships, revealing when negativity can escalate to a point of no return. This equation helps anticipate the likelihood of a relationship ending.
Breaking Down the Equation
The equation's left side measures the wife's next emotional response. It depends on her overall mood (w), her mood with her husband (rwWt), and crucially, how her husband's actions influence her (IHM). Ht in parentheses signifies that this influence hinges on the husband's recent behavior.
The husband's equation follows a parallel structure: h, rHHt, and IHM represent his mood alone, with his wife, and the influence his wife exerts on his subsequent response.
The Power of Mutual Influence
The most critical element impacting a couple's well-being is the mutual influence they have on each other. Researchers observed that when a husband expresses positivity towards his wife or their life together, the wife responds positively in return. Conversely, negativity tends to breed more negativity in this delicate dance of emotions.
Math and Love: Unveiling Surprising Patterns
It's intriguing to discover that these equations, originally devised for love, can also describe international relations during arms races. Mathematically, spiraling into negativity before a breakup parallels a potentially catastrophic scenario, akin to a nuclear war in international relations. Love's dynamic interaction can be illustrated graphically.

The Surprising Compromise
Contrary to intuition, research shows that maintaining a healthy relationship isn't about having a high negativity threshold (where you only address big issues). It's quite the opposite.
The Power of Mathematical Models
Mathematical models can't find "the one" or guarantee perfect relationships. Instead, they extract insights from reality, helping us grasp the inner workings of relationships and uncover counterintuitive outcomes in the real world.
A Positive Message
In the end, mathematics leaves us with a positive message for our relationships: don't let conflicts fester, reinforcing the age-old wisdom of not going to bed angry.